In part 2 we are going focus on checking our assumptions. So far we have learned how to perform a K Means Cluster. When running a K Means Cluster, you first have to choose how many clusters you want. But what is the optimal number of clusters? This is the “art” part of an algorithm like this.
One thing you can do is check the distance from you points to the cluster center. We can measure this using the interia_ function from scikit learn.
Let’s start by building our K Means Cluster:
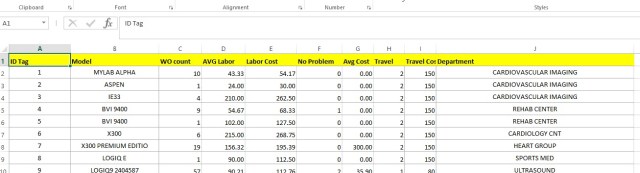
Import the data
import pandas as pd
df = pd.read_excel("C:\Users\Benjamin\Documents\KMeans1.xlsx")
df.head()

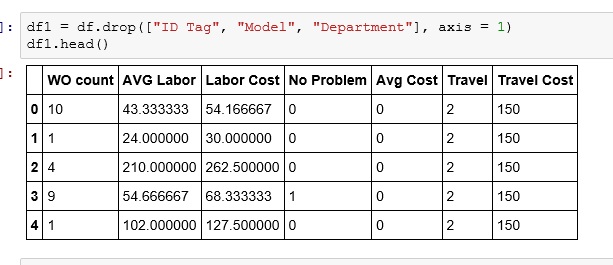
Drop unneeded columns
df1 = df.drop(["ID Tag", "Model", "Department"], axis = 1) df1.head()
Create the model – here I set clusters to 4
from sklearn.cluster import KMeans km = KMeans(n_clusters=4, init='k-means++', n_init=10)
Now fit the model and run the interia_ function
km.fit(df1) km.inertia_

Now the answer you get is the sum of distances from your sample points to the cluster center.
What does the number mean? Well, on its own, not much. What you need to do is look at a list of interia_ for a range of cluster choices.
To do so, I am set up a for loop.
n = int(raw_input("Enter Starting Cluster: "))
n1 = int(raw_input("Enter Ending Cluster: "))
for i in range(n,n1):
km = KMeans(n_clusters=i, init='k-means++', n_init=10)
km.fit(df1)
print i, km.inertia_

The trick to reading the results is look for the point of diminishing returns. The area I am pointing to with the arrow is where I would look. The changes in values start slowing down here.
I am using this example because I feel it is more real world. Working with real data takes time to a get a feeling for. If you are having trouble seeing why I chose this point, consider the following textbook example:
See how at this highlight part, the drop in number goes from hundreds to 25. That is a diminished return. The new result is not that much better than the earlier result. As opposed to 1 and 2 where 2 clusters perform 1000 units better.