IBM’s CPLEX is a commercial quality Optimization product. It can handle 10’s of 1000’s of variables as well as massive data sets. As with most commercial software it is very expensive, but they do offer a limited edition you can download to get some experience working with it.
You can find the free downloads here: CPLEX Download
In this example, we will be using CPLEX OPL (optimization programming language) to solve a very simple linear problem. Check out the already solved solution below:
As you can see, we are deciding which of 2 types of furniture, Table and Chairs. Our goal is maximize our profit, however we only have 300 units of material and 110 units of labor available.

Let’s break it down into some basic formulas now.
First, what are the two main elements we have here? Furniture (Table, Chair) and Resources (Material and Labor). All other elements are related to either Furniture or Resources in some way.
How Many? is related to Furniture. To make this easier to follow we will shorten How Many? to HM
Profit per Unit is also related to furniture – let’s call it P
So Total Profit = HM[Table]*P[Table] + HM[Chair]+P[Chair]
In a bit more formal format: 
Coding in CPLEX
Now let’s code this in CPLEX. First we need to create a new OPL Project

Name your project and make sure to check Create Model and Create Data

You will note you now have two new files, a .mod and .dat
- .mod = model file
- .dat = data file

We are going to start by building our model file.
The model file consists of 4 parts
- Variable declaration
- Decision variable declaration
- Objective
- Constraints
Variable Declaration
{string} furniture = ...;
{string} resources = ...;
int P[furniture] = ...;
int Avail[resources] = ...;
int ResValue[resources][furniture] = ...;
First- the =…; means the variable will find its values in the .dat file. We will get there soon.
{string} furniture = …; — blue box
{string} resources = …; — red box

int P[furniture] = …; – red box
int Avail[resources] = …; – green box
int ResValues[resources][furniture] = …; – purple box

The [] after the variable name tells which string the variable is related to. If you having trouble seeing what I am talking about, look at the images below.



I know this is confusing, but hopefully it will clear up as we move forward.
Decision variable declaration
dvar int HM[furniture];
Our decision variable (dvar) is how many units to build (HM). This is of course related to furniture. As the picture below shows:

Objective:
maximize sum(i in furniture) HM[i]*P[i];
Our object is to maximize profit. The equation above is simply the OPL way of writing:
HM[Table]*P[Table] + HM[Chair]+P[Chair]
sum(i in furniture) is like a for loop where the results of each iteration are summed up. The two values passed through i would be Table and Chair.
Constraints:
subject to {
forall(i in resources)
ct1:
sum(j in furniture)
ResValue[i][j]*HM[j]<=Avail[i];
}
Our final chunk of code in our model (.mod) file is our Constraints. Constraints are started by using the code: subject to {}
Forall(i in resources) – is just a for loop iterating through (materials, labor)
ct1: – just names your constraint – an issue in bigger problems where you might have many constraints.
To clarify I will walk you through the sum(j in furniture) loop.
- ResValue[Materials][Table]*HM[Table]<=Avail[Materials]
- ResValue[Materials][Chair]*HM[Chair]<=Avail[Materials]
- ResValue[Labor][Table]*HM[Table]<=Avail[Labor]
- ResValue[Labor][Chair]*HM[Chair]<=Avail[Labor]
Here is what the code looks like in CPLEX

Now, let’s fill in our .dat (data file)
The code should be pretty self explanatory, note the use of {} for our string variables
furniture = {"Table","Chair"};
resources = {"Wood", "Labor"};
P = [6,8];
Avail = [300,110];
ResValue = [[30,20],[5,10]];
Here is the code in CPLEX

Run the code
To run the code, we first need to create a running configuration. Right click on Run Configurations > New > Run Configuration

Name your run configuration

Now, select you .mod and .dat files one at a time and drag them into your new running config. When you get the pop up warning, just click okay. Repeat this task for both files
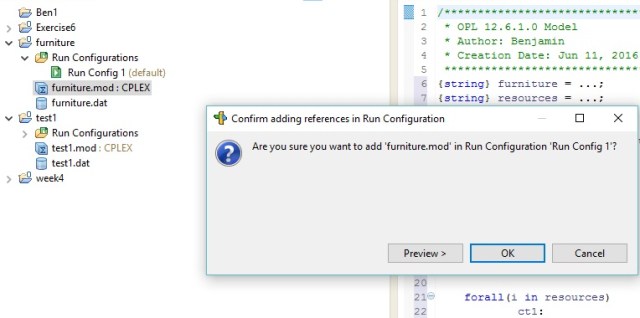
Here is what your screen should look like.

Right click your running config and click Run this

Click Okay to save your mod and dat file

And now we have our results. 96 is out total profit with 4 Tables and 9 Chairs being built. Just like our Solver solution above.

The Code
.mod file
{string} furniture = ...;
{string} resources = ...;
int P[furniture] = ...;
int Avail[resources] = ...;
int ResValue[resources][furniture] = ...;
dvar int HM[furniture];
maximize
sum(i in furniture)
P[i]*HM[i];
subject to {
forall(i in resources)
ct1:
sum(j in furniture)
ResValue[i,j]*HM[j]<=Avail[i];
}
.dat file
furniture = {"Table","Chair"};
resources = {"Wood", "Labor"};
P = [6,8];
Avail = [300,110];
ResValue = [[30,20],[5,10]];