Tag: excel solver linear programming

Linear Optimization Model: Binary Constraints

On By Ben Larson Ph.D.In excel, Optimization Modeling1 Comment

Today we are going to build a Linear Optimization Model with binary constraints. What that means is that some of our decision variables are going to be restricted to 0 or 1 as possibilities.

This example is more complicated than earlier lessons, so I have included a fully filled out Excel file for you to follow along with. You can download the Excel file here: ModelBuild

Let’s start with the problem:

You have been hired by a company that builds airplane model kits. They currently produce 5 types of models – F-16’s, F-18’s, A-10’s, B-2’s, and B-52’s. They want you to help them maximize their profits.

They have provided you with the following production information.

The Minimum production may need a little explanation. Setting up the equipment to build a particular model has an expense built in. To cover that expense, you need to commit to building at least the value found in the minimum production row. If you can’t meet this level of production, we are not going to build any of this model.

binary1.jpg

We have also been given our available resources:

binary2.jpg

So now on to our decision variables. For each model, we have to first decide whether or not to produce. Remember, if we can’t produce our minimum amount for a particular model, we can’t produce any of that model.

So our Produce? decision variables are going to be either 1 (produce) or 0 (don’t produce)

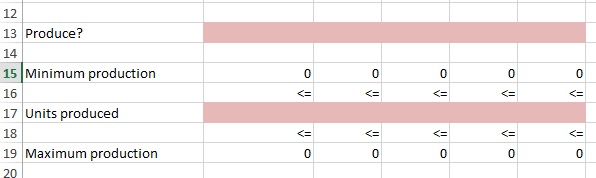
binary3.jpg

Now our Minimum production row is a simple formula= Minimum production from row 7 above * your 1 or 0 from Produce?  I have placed a 1 in the first column of our Produce? row to demonstrate below.

binary4

Skip Units produced for now. Look at Maximum produced. This formula is simply the 1 or 0 from our Produce? row * 9999. I choose 9999 at random as I know we will never exceed this limit in our example. In other models, you may need a larger number.

Now Units produced is our second decision variable. This variable needs to sit in between Minimum production and Maximum production.

Note that if our Produce? variable is 0 (don’t build) Maximum production will be 0 (Produce? * 9999= 0) . Since Units produced needs to be less than or equal to Maximum production, we cannot produce any units.

Second, since if we decide to build (1), our Minimum production will come from our given values in blue. So our Units produced will need to be greater than or equal to the Minimum production.

 

Now lets set our Resource used using SUMPRODUCT()

Press Time

binary9.jpg

Grams Plastic

binary10

Finally, we need to set our Result cell – We do this using Sumproduct()

binary5.jpg

Now we can set up our solver.

  • Objective – Profit cell
  • Changing cells – our pink rows – note you separate the two rows with a comma
  • Set our Produce? row to binary (see second picture below)
  • Set Units produced to >= Minimum production
  • Set Units produced to <= Maximum production
  • Set Press Time Resource used <= Resource available
  • Set Grams Plastic Resource used <= Resource available

binary6

binary7.jpg

 

Finally make sure you are set to Simplex LP and hit Solve

binary8.jpg

 

Excel Solver: Optimization Models: Linear Programming 1

On By Ben Larson Ph.D.In Optimization Modeling3 Comments

Let’s build a more complex model. Here is our problem:

You own a cabinet company and you are currently making 2 types of cabinets this month: wall and base. The wall cabinet sells for $300 and the base sells for $450. The wall unit cost $150 in labor to build, while the base cabinet costs $225.

The cabinets are built from a combination of plywood (which cost $11 per sq foot) and oak (which costs $15 per sq foot). The wall unit needs  5 sq ft of plywood and 1 sq ft of oak. The base unit needs 6 sq ft of plywood and 2 sq ft of oak.

You bought your materials ahead of time to get the best rate. You have 10000 sq ft of plywood and 3000 sq ft of oak available. Finally, based on previous sales records, you estimate the most you will be able to sell is 600 wall cabinets and 1200 base cabinets this month.

So you want to know – how many of each cabinet should I build to maximize my profit?

Let’s Model It

Okay, I know. This just gave you horrible flash backs to math class and word problems. But the truth is, this is what your math class was trying to prepare you for. We are going to use math to create a model that mimics the real world and solves a problem.

Open up Excel and let’s start.

***Note: I suggest you try building this model yourself first. If you need help, just follow my steps below, but only follow me as needed.

Let’s start by inputting some of the information we know:

Known Info

Prefilled Excel for Known Info: cabinet1

Price of materials:

lp1.jpg

Amount of Available Materials

lp2

Now add what we know about building the cabinets

lp3.jpg

Finally, input your build limits

lp4

Here is our model so far

lp5.jpg

Changing Variable

In this model, our changing variable is how many of each cabinet we will build.

lp6

Objective

Next, let’s set up out Objective. In our model, the object will be total profit.

lp67.jpg

Calculations

Now you need to add the calculations that will make your model work.

Excel File with Calculations: cabinet_with_equations

First let’s calculate material use. I will use SUMPRODUCT() to do this. In the example below, I am multiplying the number of cabinet types built(changing cells F9:G9) by the material requirements (plywood B7:C7)

Then repeat for oak.

lp8

Now calculate profit for each cabinet.

Here is how I did it. Selling Price – Labor Cost – (plywood cost per sq ft * sq ft used + oak price per sq ft * ft used)

I repeated for Floor cabinets

lp9.jpg

Finally I am calculating the final profit. This is done by using Sumproduct() again. This time it is sumproduct(Profit, Actual Build)

Run Solver:

Click on Data and Solver in Ribbon up top.

Now set the Objective to you Profit Cell (A15), and the Change Variables to your Build cells (PINK – F9:G9). Click Max and set the Solving Method to Simplex LP

lp11

Constraints

Hit Add to the right of the Constraints window and add your constraints

lp12

Looking at your spreadsheet, your constraints below state

  • plywood used <= plywood available
  • oak used <= oak available
  • Wall built <= max Wall Build
  • Floor built <= max Floor Build

Now Hit Solve

lp13.jpg

Check Keep Solver Solution:

Hit OK

lp14.jpg

Solution

Now you have a solution. According to Solver, you should build 560 Wall and 1200 Floor cabinets to maximize your profit.

lp15.jpg